2023. 3. 26. 01:57ㆍDATA PROGRAMMING/PYTHON
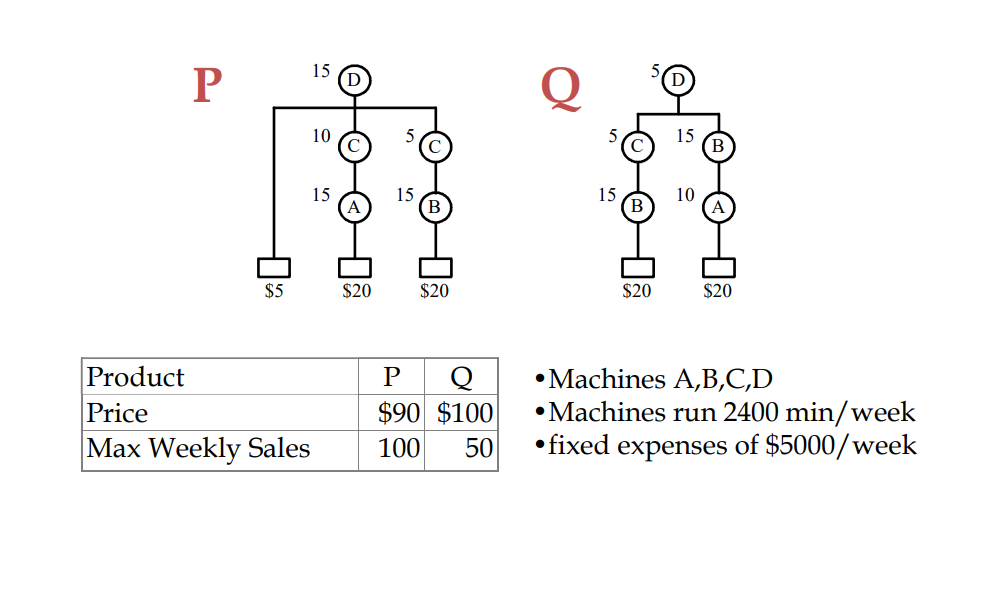
Godratt Problem은 가장 기초적인 LP(Linear Problem)이다. 조건들이 간단하기에 대수적 모형을 만드는 과정은 생략하고 엑셀로만 해결하던 LP문제의 최적해를 파이썬 OR-Tool을 이용해 구해보고자 한다.
Godratt Problem 파이썬 OR-Tool 풀이 방법

!pip install ortools #OR-tool 설치
from ortools.linear_solver import pywraplp
def main():
solver = pywraplp.Solver.CreateSolver('SCIP')
p = solver.IntVar(0, 100, 'xp')
q = solver.IntVar(0, 50, 'xq')
solver.Add(15*p + 10*q <= 2400)
solver.Add(15*p + 30*q <= 2400)
solver.Add(15*p + 5*q <= 2400)
solver.Add(15*p + 5*q <= 2400)
solver.Maximize((90-45) * p + (100-40) * q - 5000)
solver.Solve()
print('Solution:')
print('Objective value =', solver.Objective().Value())
print('x =', p.solution_value())
print('y =', q.solution_value())
if __name__ == '__main__':
main()
우선 엑셀 혹은 pywraplp.Solver.CreateSolver('GLOP')을 통해 해결한다면 각 제품의 생산량이 소수점 단위로 구해지게 된다. 그런 상황을 방지하고 생산량의 갯수를 정수해로 맞추기 위해 pywraplp.Solver.CreateSolver('SCIP')를 solver로 설정하였다.
구해야 하는 것은 두 제품의 생산량(Xp, Xq)과 최적해(최대 이익)이다. 이 때 결정변수인 Xp와 Xq값을 각각 p와 q변수에 저장해 주었다.
각 제약조건을 slover.add()함수를 통해 쉽게 생성할 수 있었다.마지막으로 최적해를 설정해 주고 코드를 실행하면 간단하게 최적 생산량과 최적해를 구할수 있었다.
느낀점
항상 엑셀로 해결하던 LP문제를 파이썬으로 해결해 보았다. 엑셀이 아닌 파이썬을 사용했을 때의 이점은 '편리함'이었다. 엑셀의 경우 스프레드 시트에 조건들을 적은 후 각 셀에 수식들을 입력하고 최적해 찾기를 통해 다시 조건을 입력하여 최적해를 찾아야 해서 문제를 한 눈에 보기위해 세팅해야 하는 과정이 길었다면 파이썬 코드를 작성하면 조건들을 작성하는 동시에 그 내용들을 한눈에 볼 수 있었기에 문제의 전체적인 양상을 관찰하면서 코드를 작성하기에 편리했다.또한 LP문제를 활용함에 있어 조건을 조금씩 수정해야 하는 과정이 필요한데 이 점 또한 엑셀보다 파이썬이 압도적으로 편리하다는 것을 느꼈다. 엑셀은 셀을 수정하고 최적해 찾기에서 다시 한 번 조건들을 수정하고 최적해 찾기를 해야 하는데 파이썬은 바로 코드를 수정한 이후에 전체적으로 빠르게 검토하고 바로 코드를 실행하며 문제를 해결해 나갈 수 있었다. 이런 점에서 문제가 복잡해 질수록 조건이나 알고리즘의 내용을 조금씩 수정하고 즉각적으로 확인하기 쉬운 파이썬을 활용하는 것이 문제 해결에 더욱 용이할 것으로 생각된다.
'DATA PROGRAMMING > PYTHON' 카테고리의 다른 글
| [Python] Class의 정확한 이해와 사용법 (0) | 2023.09.13 |
|---|---|
| 파이썬 NUMPY 이미지 파일 색깔 수정하 (0) | 2023.08.03 |
| [파이썬] 클래스가 불균형한 데이터 머신러닝 분류 모델 실습 (0) | 2023.06.04 |
| 파이썬을 통해 간단하게 학교 성적 평균, 표준편차, 백분위 구하기 (0) | 2023.05.29 |
| 파이썬 Pandas 기초부터 심화까지 - 1 (인덱싱, loc, 결측치) (0) | 2023.05.11 |